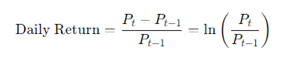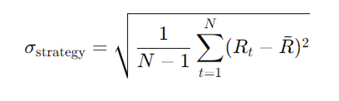Automatische Portfoliokonstruktion

Dies ist eine neue Funktion in einer neuen Portfolio Komponist Modul von StrategyQuantX. Um mehr darüber zu erfahren, besuchen Sie Portfolio Komponistund die Unterschied zwischen Portfolio Composer und Portfolio Master.

Kurz gesagt, der Portfolio Composer ermöglicht Ihnen die Simulation eines Portfolios einschließlich der Gewichtungen (wie viel Geld jeder Strategie im Portfolio zugewiesen werden soll). Sie können die Strategien auswählen, die Sie testen möchten, ihre Gewichte festlegen und auf die Schaltfläche "Portfolio neu berechnen" klicken, um eine Portfoliosimulation zu erstellen.

Automatische Berechnung des Portfolios

Die neue Funktion der Automatische Berechnung bietet hierfür einen automatisierten Ansatz. Sie brauchen die Gewichte nicht mehr manuell festzulegen - Sie können Modelle verwenden wie Effiziente Markowitz-Grenze (weitere werden hinzugefügt), um das optimale Portfolio und die Strategiegewichtung zu berechnen!

Portfolio Composer: Automatisierte Markowitz-Effizienzgrenze für optimale Strategiegewichtung

In der sich ständig weiterentwickelnden Welt des Handels erfordert die Zusammenstellung eines optimalen Portfolios von Strategien ein Gleichgewicht zwischen Renditepotenzial und akzeptablem Risikoniveau.

Portfolio Komponist führt eine neue Stufe der Automatisierung ein, indem es die Effiziente Markowitz-Grenze zur Berechnung der optimale Gewichte für jede Strategie. Diese fortschrittliche Funktion gewährleistet, dass Händler systematisch die höchstmögliche Rendite für ein bestimmtes Risikoniveau erzielen können. Durch die Automatisierung dieser komplexen Berechnungen vereinfacht der Portfolio Composer nicht nur den Portfolio-Optimierungsprozess, sondern gibt Händlern auch die Möglichkeit, datengestützte Entscheidungen mit Vertrauen zu treffen.

Was ist die Effizienzgrenze?

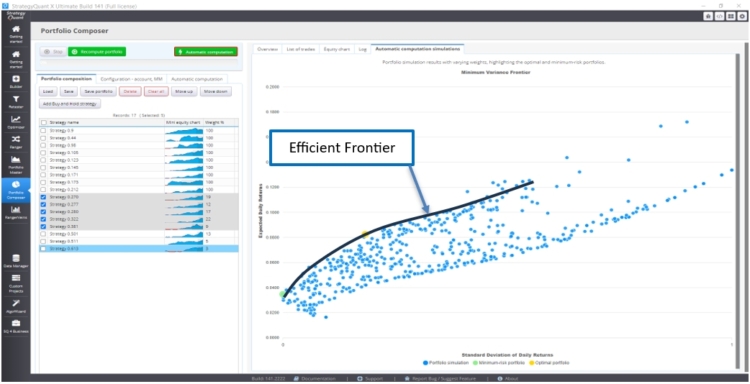
Die Effiziente Grenze ist ein Schlüsselbegriff in Moderne Portfoliotheorie (MPT) die eine Reihe optimaler Portfolios darstellt, die die höchste erwartete Rendite für ein bestimmtes Risikoniveau (oder das niedrigste Risiko für ein bestimmtes Renditeniveau) bieten. Portfolios, die auf der Effizienzgrenze liegen, dominieren diejenigen, die darunter liegen, weil sie bei gleichem Risiko bessere Renditen oder bei gleicher Rendite weniger Risiko bieten.

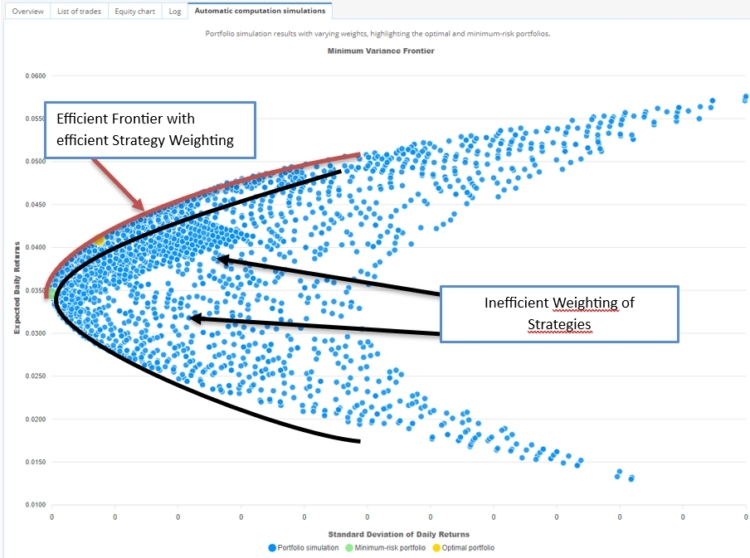
Die Effizienzgrenze wird in der Regel als Kurve in ein Diagramm eingezeichnet:

• X-Achse: Steht für das Risiko, gemessen an der Standardabweichung (Volatilität) des Portfolios.
• Y-Achse: Stellt die erwartete Rendite des Portfolios dar.

Portfolios, die unterhalb der Effizienzgrenze liegen, werden berücksichtigt ineffizientda bessere Risiko-Ertrags-Kombinationen verfügbar sind. Portfolios auf der Grenze sind optimal und werden als effizient angesehen.

Die erwartete Rendite / Standardabweichung (Volatilität) stellt die Sharpe Ratio des Portfolios dar.

Das Optimale Portfolio ist das Portfolio mit der höchsten Sharpe Ratio.

Wer hat sie geschaffen?

Die Effizienzgrenze wurde eingeführt von Harry Markowitzein amerikanischer Wirtschaftswissenschaftler, in seinem bahnbrechenden Werk zur Portfoliotheorie. Sein Papier aus dem Jahr 1952, "Portfolioauswahl", veröffentlicht in der Journal of Financelegte er den Grundstein für die moderne Portfoliotheorie. Für diese Arbeit wurde er später mit dem Nobel-Gedächtnispreis für Wirtschaftswissenschaften in 1990.

Die Effiziente Grenze basiert auf der täglichen Rendite, der Portfolio-Volatilität und dem Value at Risk:

1. Tägliche Renditeberechnung

Die tägliche Wiederkehr misst die prozentuale Veränderung des Wertes eines Vermögenswertes oder Portfolios von einem Handelstag zum nächsten. Für einen Vermögenswert wird er wie folgt berechnet:

• Pt ist der Preis des Vermögenswerts zum Zeitpunkt t.
• Pt-1 ist der Preis des Vermögenswerts am Vortag.

2. Berechnung der Volatilität der Strategie

Die Volatilität einer Strategie bezieht sich darauf, wie stark die Erträge dieser Strategie im Laufe der Zeit schwanken. Sie wird üblicherweise gemessen anhand der Standardabweichung der täglichen Renditen. Eine hohe Volatilität deutet auf größere Schwankungen der Renditen hin, während eine niedrige Volatilität auf eine stabilere Performance hindeutet. Für eine einzelne Handelsstrategie kann die tägliche Volatilität wie folgt berechnet werden:

• Rt ist die tägliche Rendite der Strategie am Tag t.
•  ist die durchschnittliche tägliche Rendite der Strategie während des Zeitraums.
• N ist die Gesamtzahl der Handelstage.
• Sigma der Strategie ist die Standardabweichung, die die Volatilität der Strategie darstellt. (oder das Risiko)

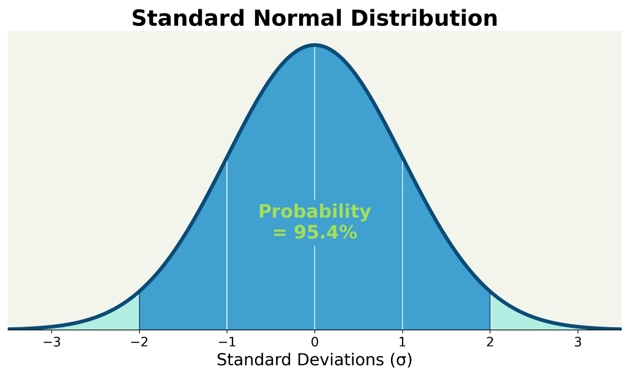
Da die Rendite um die durchschnittliche tägliche Rendite schwankt, berechnen wir die Volatilität der Strategie mit einem Konfidenzniveau von 95 %, was bedeutet, dass 95% der Punkte in diesem Bereich liegen werden und nur 5 von 100 Tagen über der berechneten Volatilität liegen könnten.

Bei dieser Berechnung wird von einer Normalverteilung der Rendite um die durchschnittliche tägliche Rendite unter normalen Marktbedingungen ausgegangen.

3. Konfidenzniveau und VaR (Value at Risk)

Bei einer 95% Vertrauensniveaukönnen wir den potenziellen Verlust des Portfolios wie folgt schätzen Value-at-Risk (VaR). Der VaR schätzt den maximalen erwarteten Verlust über einen bestimmten Zeitraum, wobei normale Marktbedingungen angenommen werden. Für ein Portfolio mit normalverteilten Renditen ist der VaR bei einem Konfidenzniveau von 95% gegeben durch:

Wo:

• 1,65 der z-score was einem Konfidenzniveau von 95% entspricht. (Verwendung einer z-Tabelle oder eines Taschenrechners zur Ermittlung des z-Scores)
• Sigma Portfolio ist die tägliche Portfolio-Volatilität.
• T ist der Zeithorizont (z. B. 1 Tag, 5 Tage).

Aus der erwarteten Rendite, der Volatilität und dem Value at Risk können wir das effizienteste Portfolio auswählen.

Anwendung im Portfolio Composer:

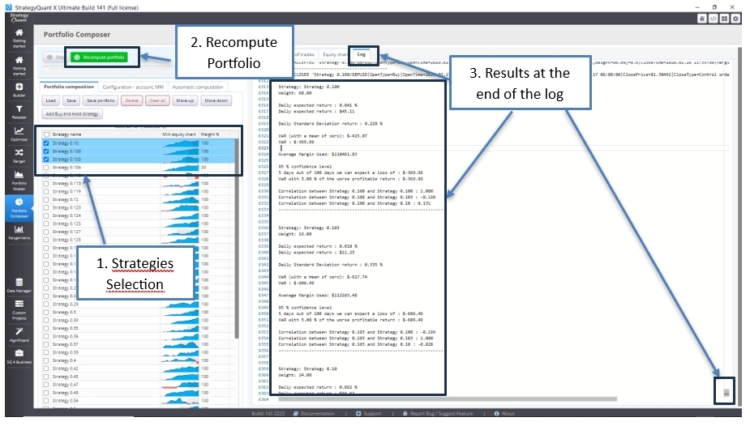
1. Erster Schritt eine Portfoliokalkulation:

Bei dieser ersten Methode wird ein Portfolio analysiert

Wenn wir einige ausgewählte Strategien neu berechnen, können wir in der letzten Zeile des Protokolls für jede Strategie lesen:

• Die tägliche erwartete Rendite
• Die tägliche Standardabweichung (das Risiko der Strategie)
• Der gefährdete Wert
• Die Korrelation zwischen Strategien

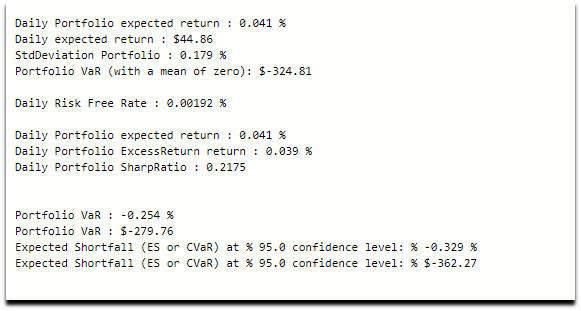
Dann können wir die Portfolio-Informationen lesen:

• Die Erwartete tägliche Rendite
• Die Tägliche Standardabweichung (das Risiko des Portfolios)
• Die Wert im Risiko des Portfolios (VaR)
• Die Sharpe-Ratio des Portfolios
• Dann wird die Erwartetes Defizit (oder der Conditional Value at Risk)

Wir fügen den erwarteten Fehlbetrag hinzu, wenn sich der Markt nicht im Normalzustand befindet und nicht der Normalverteilung entspricht.

2. Automatische Portfoliokalkulation:

Bei dieser zweiten Methode werden mehrere Portfolios mit unterschiedlichen Gewichtungskombinationen analysiert.

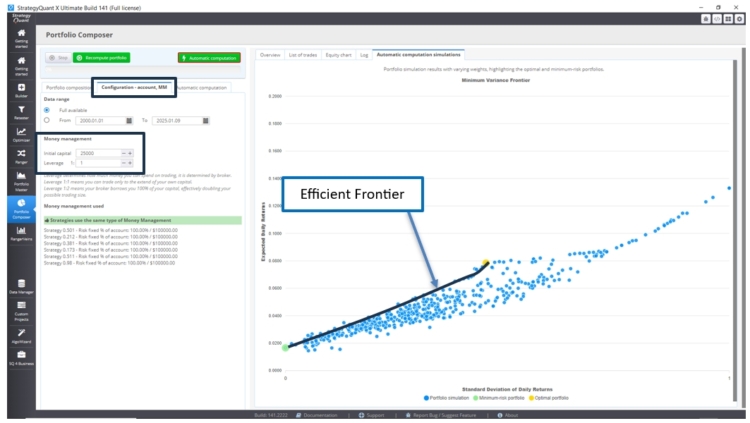
2.1 Die Sharpe-Ratio-Fitness Berechnung:

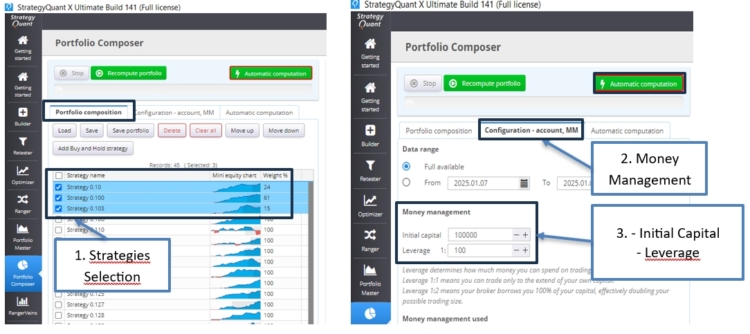
Wir können die Strategien auswählen, das Geldmanagement mit seinen Einstellungen konfigurieren und dann z. B. den Fitness-Typ und die Anzahl der Simulationen auswählen:

• Wir wählen 3 Strategien
• Auf der Registerkarte Money Management geben wir einen Hebel von 100 ein.
• Auf der Registerkarte "Automatische Berechnung" wählen wir als Fitness: Sharpe Ratio
• 500 oder 1000 Simulationen
• Der risikofreie Zinssatz, basiert auf einer Anlage mit minimalem Risiko wie Anleihen.

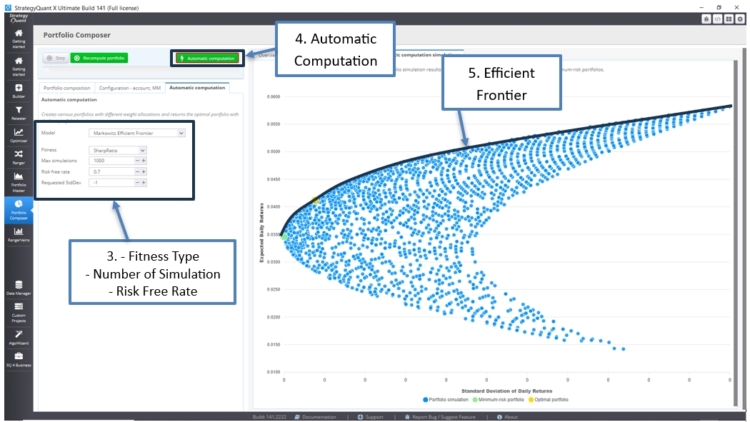
Wir erhalten die folgenden Ergebnisse: Das optimale Portfolio ist gelb hervorgehoben, da es das beste Sharpe-Ratio (Rendite/Standardabweichung) aufweist.

Außerdem ist das Portfolio mit dem geringsten Risiko grün hervorgehoben.

Die optimalen Portfolios liegen auf der Linie der Effizienzgrenze. Abhängig von der Standardabweichung (Volatilität) können wir das Portfolio wählen, das die maximale Rendite bietet.

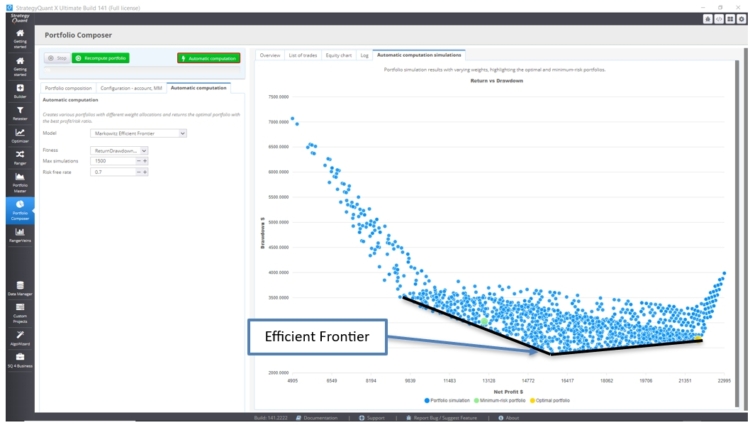
2.2 Die Rendite vs. Drawdown-Verhältnis Fitnessberechnung:

Alternativ können wir auch die Option Rendite/Drawdown-Verhältnis Fitness um eine andere Perspektive auf die Ergebnisse zu erhalten:

Das optimale Portfolio (gelb) würde den geringsten Drawdown bei maximalem Gewinn aufweisen. Wir können es mit dem Portfolio mit minimalem Risiko (in grün) vergleichen.

Die optimalen Portfolios liegen auf der Linie der Effizienzgrenze. Abhängig vom Drawdown können wir das Portfolio wählen, das den maximalen Gewinn bietet.

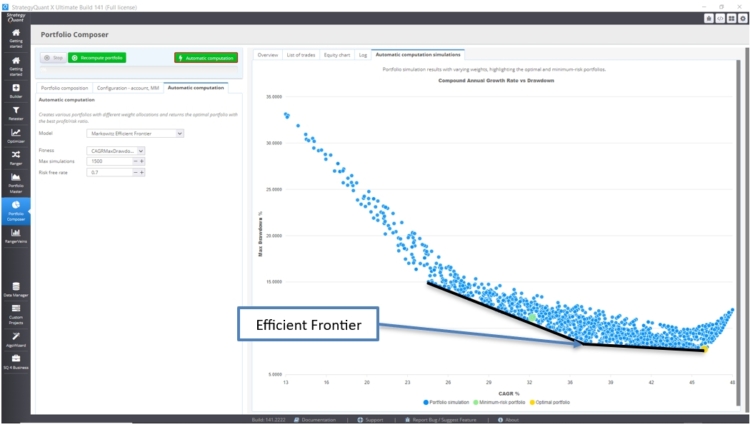
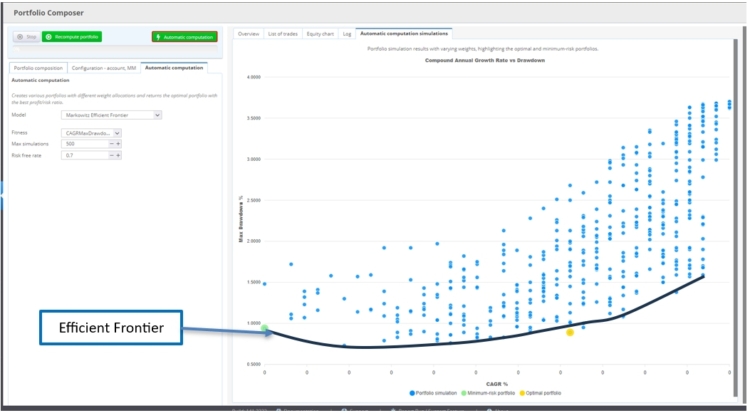
2.3 Die Jährliche Wachstumsrate vs. maximaler Drawdown Fitnessberechnung:

Verwendung von Durchschnittliche jährliche Wachstumsrate (CAGR) vs. Max Drawdown-basierte Fitness Portfoliogewichtung zu vergleichen, bietet eine gute Perspektive zwischen Langfristiges Wachstum und Risikosensitivität.

Um das optimale Portfolio zu erhalten, suchen wir nach dem höchster CAGR und niedrigster Max Drawdown. (in gelb)

Die optimalen Portfolios liegen auf der Linie der Effizienzgrenze. Je nach Drawdown können wir das Portfolio wählen, das die maximale CAGR bietet.

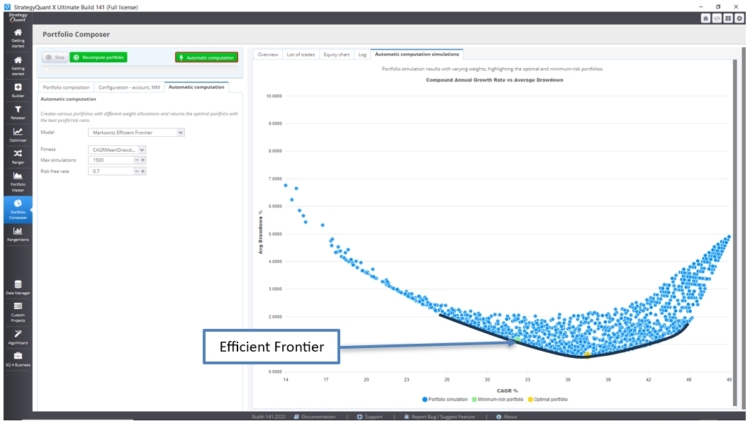
2.4 Die Jährliche Wachstumsrate im Vergleich zum durchschnittlichen Drawdown Fitnessberechnung:

Verwendung von die durchschnittliche jährliche Wachstumsrate (CAGR) im Vergleich zur durchschnittlichen Inanspruchnahme (Drawdown) weniger empfindlich auf Portfolios mit Ausreißer-Downs reagieren wird.
Die optimalen Portfolios liegen auf der Linie der Effizienzgrenze. Je nach Drawdown können wir das Portfolio wählen, das das Maximum bietet CAGR.

3. AlgoCloud Stockpicker

Für AlgoCloud Stockpicker, in der Rubrik "Konfiguration - Konto MMRegisterkarte ", sollte die Hebelwirkung auf 1 gesetzt werden, da wir mit Aktien handeln. Ein Anfangskapital von $25.000 kann als Ausgangspunkt für die Optimierung verwendet werden.

Die Form der Effizienzgrenze wird etwas anders sein, da wir mit optimierten Strategien arbeiten, die über mehrere Instrumente hinweg handeln.

Da jede Strategie Hunderte von Instrumenten umfasst, ist für die Optimierung mehr Zeit erforderlich, wenn mehrere Strategien verwendet werden.

Hier ist die Effiziente Grenze der Sharpe Ratio Fitness:

Hier ist die Effiziente Grenze der CAGR Max Draw Down Fitness:

Hier ist die Effiziente Grenze der Rendite vs. Drawdown Fitness:

Als Referenz und zum besseren Verständnis:

Bücher

• "Portfolio Selection" von Harry Markowitz, Teil III: "Efficient Portfolios", Kapitel VII: "Geometric Analysis" (Yale University Press)
  Ein Auszug
• "Modern Portfolio Theory and Investment Analysis" von Edwin Elton, Martin Gruber, Stephen Brown und William Goetzmann (Wiley Custom Publishing), Teil II: "Portfolio Analysis", Kapitel 6, 9 und 11: "Techniques for Calculating the Efficient Frontier".
• "The Complete Guide to Portfolio Performance" von Pascal François und Georges Hubner (Wiley Custom Publishing), mit dem Kapitel "Classical Performance Measures Revisited" (Kapitel 6)
• "Intelligente Portfolios" und "Systematischer Handel" von Robert Carver

Hinweis: Wir haben weitere gute Bücher von Harry Markowitz und anderen, die jedoch eher theoretisch sind.

Im Internet

• Die Effizienzgrenze:
  Investopedia - Effiziente Grenze
  Institut für Unternehmensfinanzierung - Efficient Frontier

Darwinex und Ryan O'Connell haben auf YouTube hervorragende Videos über Portfolio-Optimierung und die Effizienzgrenze gemacht.

• Das Konfidenzintervall:
  Scribbr - Konfidenzintervall
• Um die Z-Variable aus einem Konfidenzniveau zu erhalten:
  Study.com - Wie man den kritischen Z-Wert findet